常见位运算

发表于 |

位运算简介（WIKI）

Bit manipulation is the act of algorithmically manipulating bits or other pieces of data shorter than a word. 需要进行位运算的程序包括：低层设备控制、错误检测、校正算法、数据压缩、加密算法和一些优化。 For most other tasks, modern programming languages allow the programmer to work directly with abstractions instead of bits that represent those abstractions. Source code that does bit manipulation makes use of the bitwise operations: AND, OR, XOR, NOT, and bit shifts.

在某些情况下，位操作可以消除或减少在数据结构上使用的循环，同时因为位操作是并行处理的，所以使用位运算可以成倍的提高代码运行的速度。但是，使用位运算可能会导致代码变得更加难以编写和维护。

位运算基本操作

  1. Set union A | B
  2. Set intersection A & B
  3. Set subtraction A & ~B
  4. Set negation ALL_BITS ^ A or ~A
  5. Set bit A |= 1 << bit
  6. Clear bit A &= ~(1 << bit)
  7. Test bit (A & 1 << bit) != 0
  8. Extract last bit A&-A or A&~(A-1) or x^(x&(x-1))
  9. Remove last bit A&(A-1)
  10. Get all 1-bits ~0

Bit操作实例

Count the number of ones in the binary representation of the given number

1
2
3
4
5
6
7
int count_one(int n) {
    while(n) {
        n = n & (n-1);
        count++;
    }
    return count;
}

n-1意思是：从后向前，找到最后一个不为0的bit，把它置为0；从后向前，把末尾所有的0都置为1。

n & (n -1) 可以理解为移除从后向前的第一个1。

count one

Is power of four

1
2
3
bool isPowerOfFour(int n) {
    return (n & (n - 1)) == 0 && (n & 0x55555555) != 0;
}

首先，为4的幂次的数有一个特点就是只有一位是1，且这个1要出现在奇数位上，例如：1: 1, 4: 100, 16: 10000。所以首先要判断1的个数是否是1个，然后再判断1的位置是否在奇数位上。

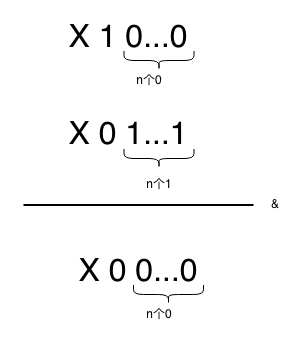
n & (n - 1) == 0 表示n的二进制表示中，只有一位是1，其余位数全为0。

n & 0x55555555 表示保留所有奇数位的数值，并将偶数位的数值置为0，因为5的二进制表示是0101。 (n & 0x55555555) != 0 表示奇数位上并不都是0。

n & (n - 1) == 0 && (n & 0x55555555) 的意思是：二进制表示的数中只有一位是1，并且这个1在奇数位上。

Sum of Two Integers

1
2
3
int getSum(int a, int b) {
    return b==0? a:getSum(a^b, (a&b)<<1); //be careful about the terminating condition;
}

和笔算加法相同。对于二进制数的而言，对应位相加就可以使用异或（xor）操作，计算进位就可以使用与（and）操作，在下一步进行对应位相加前，对进位数使用移位操作（<<）。

Missing Number

Given an array containing n distinct numbers taken from 0, 1, 2, …, n, find the one that is missing from the array. For example, Given nums = [0, 1, 3] return 2. (Of course, you can do this by math.)

1
2
3
4
5
6
7
8
int missingNumber(vector<int>& nums) {
    int ret = 0;
    for(int i = 0; i < nums.size(); ++i) {
        ret ^= i;
        ret ^= nums[i];
    }
    return ret^=nums.size();
}

利用了A xor A = 0 这个性质。

Keep as many 1-bits as possible

Find the largest power of 2 (most significant bit in binary form), which is less than or equal to the given number N.

1
2
3
4
5
6
7
8
9
long largest_power(long N) {
    //changing all right side bits to 1.
    N = N | (N>>1);
    N = N | (N>>2);
    N = N | (N>>4);
    N = N | (N>>8);
    N = N | (N>>16);
    return (N+1)>>1;
}

将首位1后面的所有位变成1。然后 + 1 再右移1位。

N = N | (N>>1); 相当于把首位的1复制一下，这样就保证了首位是11.
N = N | (N>>2); 相当于把首位的11复制一下，这样就保证了首位是1111.
N = N | (N>>4); 相当于把首位的1111复制一下，这样就保证了首位是11111111.
N = N | (N>>8); 相当于把首位的8个1复制一下，这样就保证了首位有16个1.
N = N | (N>>16); 相当于把首位的16个1复制一下，这样就保证了首位32个1.

对于int64的整型来说，正数有32位，上述做法能够保证32位正整数有效。

Reverse Bits

Reverse bits of a given 32 bits unsigned integer.

1
2
3
4
5
6
7
8
9
10

uint32_t reverseBits(uint32_t n) {
    unsigned int mask = 1<<31, res = 0;
    for(int i = 0; i < 32; ++i) {
        if(n & 1) res |= mask;
        mask >>= 1;
        n >>= 1;
    }
    return res;
}

Bitwise AND of Numbers Range

Given a range [m, n] where 0 <= m <= n <= 2147483647, return the bitwise AND of all numbers in this range, inclusive. For example, given the range [5, 7], you should return 4.

1
2
3
4
5
6
7
8
9
int rangeBitwiseAnd(int m, int n) {
    int a = 0;
    while(m != n) {
        m >>= 1;
        n >>= 1;
        a++;
    }
    return m<<a;
}

如果位数不同的话，那么所有数按位AND操作的话结果是0。

中间的循环，目的就是为了找到m和n首部相同的部分（共有多少位相同，例如5：101、7:111，只有首位相同，那么结果为 1 << 2 = 4）。

Majority Element

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times. (bit-counting as a usual way, but here we actually also can adopt sorting and Moore Voting Algorithm)

1
2
3
4
5
6
7
8
9
10
11
12
int majorityElement(vector<int>& nums) {
    int len = sizeof(int) * 8, size = nums.size();
    int count = 0, mask = 1, ret = 0;
    for(int i = 0; i < len; ++i) {
        count = 0;
        for(int j = 0; j < size; ++j)
            if(mask & nums[j]) count++;
        if(count > size/2) ret |= mask;
        mask <<= 1;
    }
    return ret;
}

Single Number III

Given an array of integers, every element appears three times except for one. Find that single one. (Still this type can be solved by bit-counting easily.) But we are going to solve it by digital logic design

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//inspired by logical circuit design and boolean algebra;
//counter - unit of 3;
//current   incoming  next
//a b            c    a b
//0 0            0    0 0
//0 1            0    0 1
//1 0            0    1 0
//0 0            1    0 1
//0 1            1    1 0
//1 0            1    0 0
//a = a&~b&~c + ~a&b&c;
//b = ~a&b&~c + ~a&~b&c;
//return a|b since the single number can appear once or twice;
int singleNumber(vector<int>& nums) {
    int t = 0, a = 0, b = 0;
    for(int i = 0; i < nums.size(); ++i) {
        t = (a&~b&~nums[i]) | (~a&b&nums[i]);
        b = (~a&b&~nums[i]) | (~a&~b&nums[i]);
        a = t;
    }
    return a | b;
}

reference